Associar essas definições algébricas com desenhos geométricos, possibilita ao aluno compreender melhor como aplicar tais propriedades e como elas são derivadas.
O estudo da Álgebra desde as definições e conceitos mais simples, sempre causa confusão na mente de estudantes, principalmente os de nível fundamental, que começam a estudar operações com números e letras, deixando-os ainda mais confusos.

Nas últimas aulas que ministrei neste bimestre, "sofri" um pouco para fazer alguns alunos entenderem determinados produtos notáveis (produto: resultado de uma multiplicação, notável: digno de nota). Pensando nisso, resolvi escrever esse artigo para mostrar algumas operações algébricas de forma diferente, fazendo uso da Geometria.
Antes as propriedade básicas, que são essenciais em todos os processos.
 |
| Associatividade |
 |
| Comutatividade |
Fator comum
Regra prática: Colocar o termo semelhante em evidência, transformando em um produto.
Forma algébrica: $ax+ay+az=a(x+y+z)$
Quadrado da soma de dois termos
Regra prática: Quadrado do primeiro termo, mais duas vezes o primeiro termo vezes o segundo termo, mais o quadrado do segundo termo.
Forma algébrica: $(a+b)^{2}=a^{2}+2ab+b^{2}$
Forma geométrica:
A pergunta que mais ouço: Por que na regra prática aparece $2$ ao lado de $a.b$? A resposta mais óbvia pode ser comprovada observando as áreas dos retângulos de cor laranja.
Trinômio quadrado perfeito
Quadrado da diferença de dois termos
Regra prática: Quadrado do primeiro termo, menos duas vezes o primeiro termo vezes o segundo termo, mais o quadrado do segundo termo.
Forma algébrica: $(a-b)^{2}=a^{2}-2ab+b^{2}$
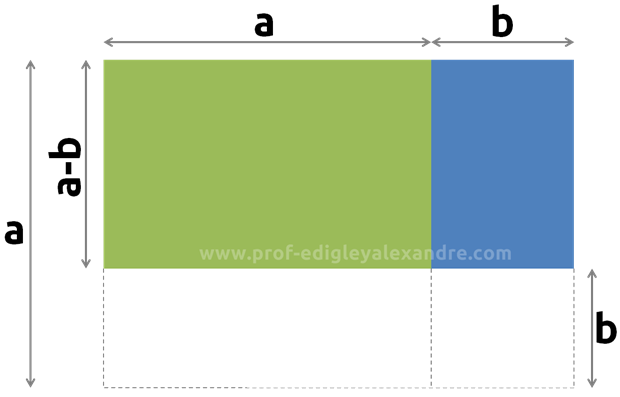
Forma geométrica:
Note que, geometricamente, a área da região verde (de lado $a-b$) é igual a área do quadrado maior (de lado $a$), menos os dois retângulos de cor laranja (de lados $b$ e $a-b$) somados com a área do quadrado azul (de lado $b$).
Em linguagem algébrica: $(a-b)^{2}=a^{2}-[b(a-b)+b(a-b)+b^{2}]$
Em uma linguagem mais simples, se "cortássemos" as regiões de cor laranja e a azul, sobraria o quadrado de cor verde, comprovando o produto notável.
Observe o desenvolvimento da expressão acima.
$(a-b)^{2}=a^{2}-[b(a-b)+b(a-b)+b^{2}]$
$(a-b)^{2}=a^{2}-[2b(a-b)+b^{2}]$
$(a-b)^{2}=a^{2}-[2ab-2b^{2}+b^{2}]$
$(a-b)^{2}=a^{2}-2ab+2b^{2}-b^{2}$
$(a-b)^{2}=a^{2}-2ab+b^{2}$Produto da soma pela diferença de dois termos
Regra prática: Quadrado do primeiro termo, menos o quadrado do segundo termo.
Forma algébrica: $(a+b)(a-b)=a^{2}-b^{2}$
Forma geométrica:
Qual a área do retângulo formado pelas cores verde e azul?
Somando as áreas de cor verde e azul, é possível comprovar esse produto notável. Assim:
$(a-b)a+(a-b)b=$
$a^{2}-ab+ab-b^{2}=$
$a^{2}-b^{2}$
Comprovando que $(a+b).(a-b)=a^{2}-b^{2}$.
Diferença de dois quadrados
Regra prática: Primeiro termo do primeiro fator, vezes o primeiro termo do segundo fator. Segundo termo do primeiro fator, vezes o segundo termo do segundo fator.
Forma algébrica: $a^{2}-b^{2}=(a+b)(a-b)$
Forma geométrica:
Esse processo é análogo ao Produto da soma pela diferença de dois termos.
Cubo da soma de dois termos
Regra prática: Cubo do primeiro termo mais três vezes o quadrado do primeiro termo vezes o segundo termo, mais 3 vezes o primeiro termo vezes o quadrado do segundo termo, mais o cubo do segundo termo.
Forma algébrica: $(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
Forma geométrica:
Imagem: Wikipédia
Download do material
Uma outra ideia é de confeccionar todas essas figuras em cartolinas espessas, para trabalhar essas operações como um quebra-cabeça. Além de visualizar essas operações na forma geométrica, poder manipulá-la trará mais benefícios ao aprendizado do aluno.
Quem se interessar em confeccionar essas imagens, ampliando-as, disponibilizo para download todas elas, dentro de um documento do PowerPoint 2007 (na época que ainda usava o Windows). Escolha um dos servidores abaixo para salvar gratuitamente em seu computador.


















Muito bom Mesmo excelente, me ajudou bastante(andre aki é o vitor)
ResponderExcluirOlá, Vitor!
ExcluirEsse era o objetivo. Se te ajudou, compartilhe o que aprendeu com os seus colegas.
Um abraço!
Professor, parabéns! Muito esclarecedor e útil. A única novidade para mim foi a forma geométrica que não é e nem foi explanada pelos professores do meu colégio até a série em que eu estou. Vou recomendar às minha amigas que assim como eu não saem da sala de aula satisfeitas.
ResponderExcluirOlá, Estér!
ExcluirSabe aquele frase: "Quer que eu desenhe?". Cabe bem agora nas aulas de Matemática, quando não conseguimos entender este assunto.
Analisando os desenhos com calma é possível entendê-los e posteriormente, na forma algébrica também.
Obrigado por compartilhar.
Um abraço!
sensacional!
ResponderExcluirAjuda muito ne!
ExcluirAbraço!
Muito boa a aul!!! Até hj tenho dificuldade em visualizar essas relações, mas agora ficou mais fácil. VLW
ResponderExcluirOlá, Silmi's! Tudo bem?
ExcluirFico feliz em saber que o post te ajudou.
Um abraço e bons estudos.